Absolute Value of Complex Numbers

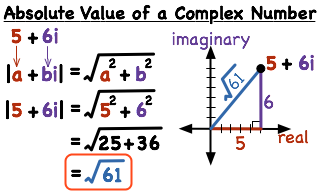
As for this lesson, it is to easy it doesn't need that much thinking; you just need to follow one simple rule, see the image above, it shows that rule which is that the absolute value equals square root a^(2) + b^(2), as for A and B, if you remeber we said that the Complex Number looks like this; a + bi, where " a " stands for the Real Number and " b " stand for the Imaginary Number beside the Imaginary unit " i ". All you have to do is to write a square root ( √ ) and then under it; write the value of " a " as a^(2) and the number beside " i ", which is " b " as b^(2), then add the value of a^(2) and b^(2) together and keep the square root.

For instance, the example in the image above, all what happened we took from the Complex Number 5+6i the " a " that equals 5 and the " b " that equals 6 and wrote them under the square root like this: 5^(2) + 6^(2) and then added them, giving us the answer √61 .