Multiplying Complex Numbers

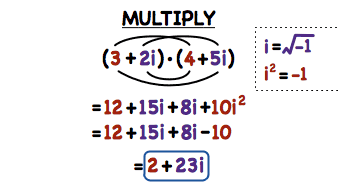
Multiplying Complex Numbers can be done with 2 ways, First multiply every term in the first equation with all terms in the second equation and add alike terms also called Distribution, the second way is called Means and Extremes, it is multiplying the first terms with each other from both equations, next multiply the second terms with each other from both equations, then multiply the far terms with each other and the close terms with each other from both equations and add alike terms together to find the result.

Lets work with equation shown in the image, we have (3+2i) x (4+5i) and we are going to use the first method, 3 x (4+5i) = 12+15i and 2i x (4+5i) = 8i+10i^(2) the i^(2)=-1 so we will replace it with -1 and multiply it with 10 giving us -10+8i, now time to add alike terms, the result will be 2+23i. As for Means and Extremes lets multiply the first terms together; 3 x 4 = 12; next the second terms; 2i x 5i = 10i^(2) which is -10 since "i^(2)" equals -1; then far terms 2i x 4 = 8i, at last close terms 3 x 5i = 15i. now add all alike terms and the result will also be 2+23i.

Notes: Imaginary unit
i^(2) = -1
i^(3) = -i
i^(4) = 1
If you find these powers, replace them with their values except for i = √-1 since we need an Imaginary part .