Subtracting Complex Numbers

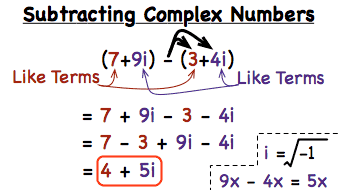
Subtracting is really simple, but you have to pay attention to the signs, because when you subtratct, you will need to use distribution for the - sign on the the equation after it, here is a Demo, the problem will be written like the following: (a+bi)-(c+di), see the " - " sign, distribute it on c+di (of course you know that negative x negative equals positive and positive x negative equals negative), so the equation will turn into -c-di, then add alike the terms and see the result after doing the Distribution.

Lets have an example, Look at the eqution on the image up there, we have (7+9i) - (3+4i); first of all, 7+9i will go out of the brackets normal as it is sice there is no negative sign before it, but 3+4i has a negative sign before it, so we will multiply the negative sign with what is in the brackets turning it into -3-4i, after adding the alike terms together we end up the result 4+5i. You might also have a question, what if it was (7+9i) - (-3-4i) in the first place, then the same steps except this time it is the negative sign multiplied by -3-4i, since we know negative x negative = positive, it will be 3+4i, add the alike terms and the result will be 10+13i.

Reminder: Keep an eye out to the sign always.